数学：贝叶斯定理的直观证明

数图结合：贝叶斯定理的直观证明

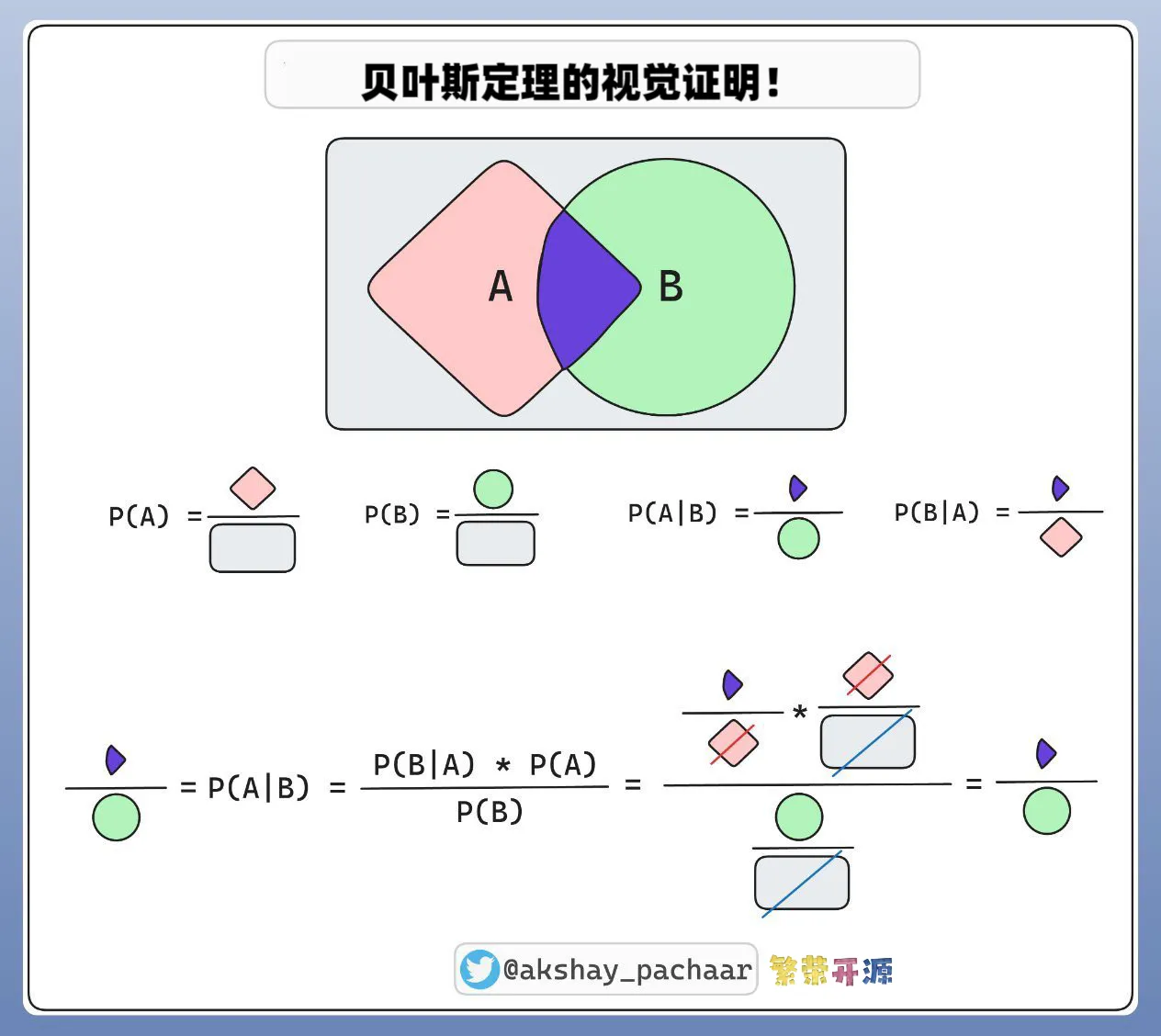
这张图展示了贝叶斯定理的几何解释，帮助我们理解条件概率之间的关系。

1️⃣区域表示：
🔸红色区域代表事件A。
🔸绿色区域代表事件B。
🔸紫色重叠区域代表同时发生A和B。

2️⃣概率定义：
🔸( P(A) ) 是事件A发生的概率，由红色区域表示。
🔸( P(B) ) 是事件B发生的概率，由绿色区域表示。
🔸( P(A|B) ) 是在B发生情况下A发生的概率，由紫色重叠部分与整个绿色区域的比值表示。
🔸( P(B|A) ) 是在A发生情况下B发生的概率，由紫色重叠部分与整个红色区域的比值表示。

3️⃣贝叶斯定理公式：

P(A|B) = frac{P(B|A) cdot P(A)}{P(B)}

图中通过几何形状和比例展示了这一公式如何成立。

这幅图通过简单的几何图形，将复杂的数学概念直观化，使得贝叶斯定理更易于理解和应用。

总结

💡 贝叶斯定理是一个数学公式，用于根据新的证据或数据更新对某一假设的概率估计。它允许我们计算在已知某些其他概率的情况下，某一事件发生的条件概率。

参考文献或转载相关：