在深度学习的广阔天地里，神经网络如同一座复杂而精密的城堡，而梯度下降、损失函数和激活函数则是这座城堡中不可或缺的基石。今天，我们将一起踏上这场优化之旅，揭开它们神秘的面纱。

一、前向传播（Forward Propagation）

定义与过程

前向传播是神经网络进行预测或分类的基础过程。它从输入层开始，通过网络的每一层逐层计算每个神经元的输出，直到到达输出层并生成最终的预测结果。这个过程中，每一层的输入是上一层的输出，每一层的输出则是下一层的输入，如此逐层传递，直到输出层。如下图：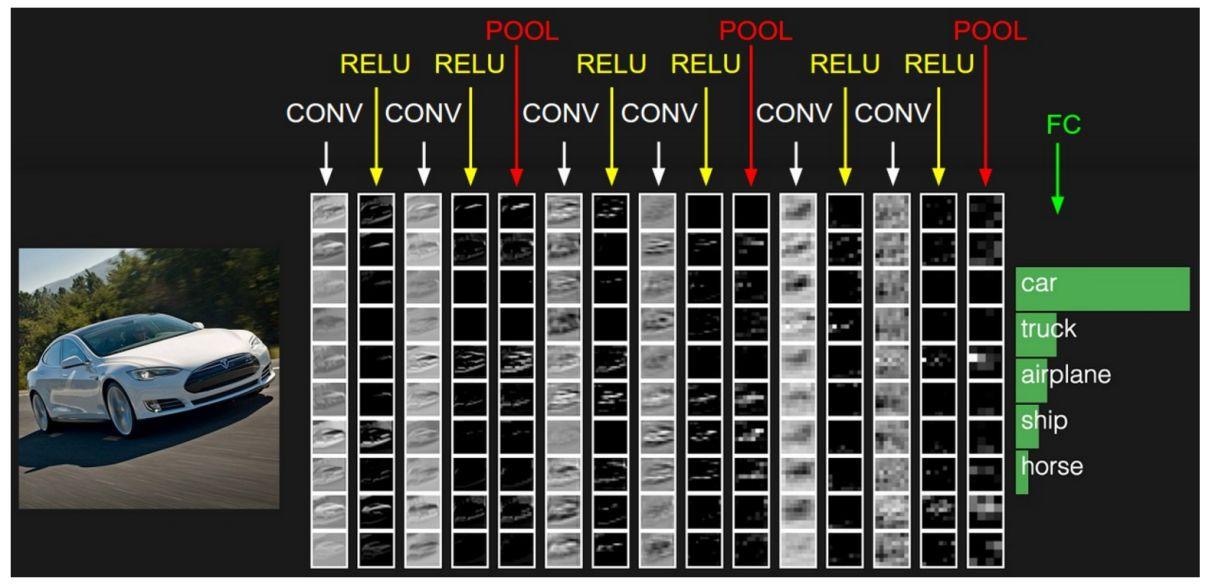
alt text

重要性

预测与分类：在推理阶段，神经网络仅使用前向传播过程来生成预测结果。输入数据通过网络进行前向传播，直到输出层生成最终的预测结果。
损失计算：在训练阶段，前向传播用于生成预测结果，这些预测结果与真实标签进行比较，从而计算出损失函数的值。这个损失值反映了模型当前的表现，是后续反向传播和参数更新的基础。
3. 计算细节

在前向传播过程中，每个神经元的输出通常是通过加权求和（即输入值与权重的乘积之和）后，再经过一个非线性激活函数得到的。这个非线性激活函数（如ReLU、sigmoid等）为神经网络引入了非线性特性，使得神经网络能够拟合复杂的函数关系。

二、反向传播（Back Propagation）

定义与背景

反向传播算法是深度学习中最为核心和常用的优化算法之一，由Rumelhart、Hinton和Williams等人在1986年提出。在BP算法出现之前，多层神经网络的训练一直是一个难题，因为无法有效地计算每个参数对于损失函数的梯度。BP算法通过反向传播梯度，利用链式法则逐层计算每个参数的梯度，从而实现了多层神经网络的训练。

工作原理

反向传播算法通过链式法则从输出层到输入层逐层计算误差梯度，并利用这些梯度更新网络参数以最小化损失函数。具体过程如下：

误差计算：从输出层开始，根据损失函数计算输出层的误差（即预测值与真实值之间的差异）。
误差传播：将误差信息反向传播到隐藏层，逐层计算每个神经元的误差梯度。这个过程中，每个神经元的误差梯度是通过链式法则与前面神经元的误差梯度相联系的。
参数更新：利用计算得到的误差梯度，可以进一步计算每个权重和偏置参数对于损失函数的梯度。然后，根据这些梯度信息，使用梯度下降或其他优化算法来更新网络中的权重和偏置参数，以最小化损失函数。

重要性

反向传播算法是神经网络训练的核心，它使得神经网络能够通过不断学习和调整参数来拟合复杂的函数关系，从而提高模型的预测准确性。

三、梯度（Gradient）

定义

梯度是一个向量，它表示函数在某一点上沿各个方向的变化率。在深度学习中，梯度通常用于表示损失函数相对于网络参数的导数（或偏导数），即损失函数值随参数变化而变化的快慢和方向。

计算方法

梯度的计算通常通过自动微分技术实现。自动微分利用计算图（Computational Graph）和链式法则自动计算梯度。计算图是一种表示函数计算过程的有向图，其中每个节点表示一个操作（如加法、乘法、激活函数等），每个边表示操作之间的依赖关系。在前向传播过程中，计算图记录了每个节点的输出和中间结果；在反向传播过程中，利用链式法则逐层计算每个节点的梯度，并将梯度传播到前面的节点。

重要性

梯度是优化算法（如梯度下降）的基础。通过计算梯度，我们可以确定参数更新的方向（即应该增加还是减少参数值）和步长（即参数更新的幅度），从而最小化损失函数并提高模型的预测准确性。

梯度消失与梯度爆炸

在深度学习中，梯度消失和梯度爆炸是两个常见的问题。梯度消失是指随着网络层数的增加，梯度值逐渐减小到接近于零，导致参数更新变得非常缓慢或停止更新。梯度爆炸则是指梯度值变得非常大，导致参数更新时出现大幅度波动或不稳定。这两个问题都会影响神经网络的训练效果和性能。
5. 梯度下降(Gradient Descent)：寻找最优解的导航仪

梯度，简单来说，就是函数在某一点上变化最快的方向。想象一下你站在一座山的山顶，梯度下降算法就像是告诉你如何最快地找到下山的路径。在神经网络中，这个“山”就是我们的损失函数，而“下山”则是寻找损失函数最小值的过程。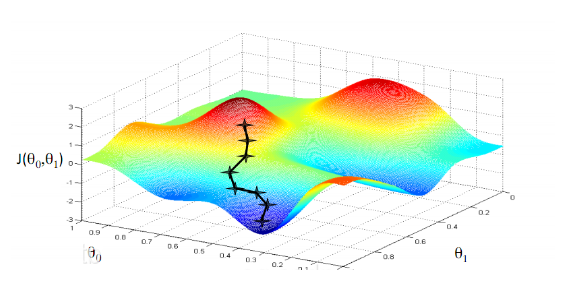
alt text

梯度下降算法的核心在于，通过计算损失函数对每个参数的梯度（即偏导数），然后沿着梯度的反方向更新参数值，以期望损失函数能够逐渐减小。这个过程中，每一步的更新幅度由学习率控制，学习率过大会导致收敛不稳定，过小则会使收敛速度过慢。

四、损失函数(loss function)及代价函数：衡量模型好坏的标尺

损失函数，顾名思义，就是用来衡量模型预测结果与实际结果之间差异的函数。在神经网络中，损失函数的选择至关重要，因为它直接决定了模型训练的方向和效果。

常见的损失函数包括均方误差（Mean Squared Error）、交叉熵损失（Cross-Entropy Loss）等。
- MSE适用于回归问题，它通过计算预测值与实际值之差的平方和来评估模型的误差；
- 交叉熵损失则更适用于分类问题，它能够有效地处理多分类问题中的类别不平衡问题。

五、激活函数(activation function)：神经元的非线性转换器

激活函数是神经网络中的另一个关键组件，它负责将神经元的输入转换为输出。没有激活函数，神经网络就只能进行线性变换，这极大地限制了其处理复杂问题的能力。
常见的激活函数包括Sigmoid、Tanh和ReLU等。

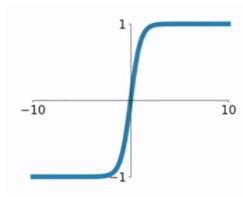
Sigmoid函数将输入映射到(0,1)区间内，适用于二分类问题的输出层；
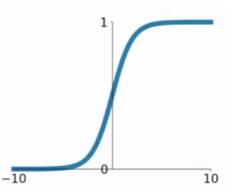
Tanh函数则是Sigmoid函数的改进版，它将输入映射到(-1,1)区间内，解决了Sigmoid函数输出不是以0为中心的问题；
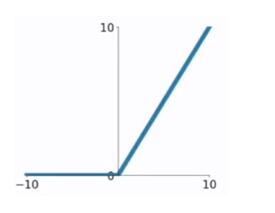
ReLU函数,又称为修正线性单元（Rectified Linear Unit），是一种分段线性函数，其弥补了sigmoid函数以及tanh函数的梯度消失问题。以其简单高效的特点在深度学习中广泛应用，它能够缓解梯度消失问题并加速训练过程。

非线性转换器又称为激活函数，激活函数的值即输出为激活值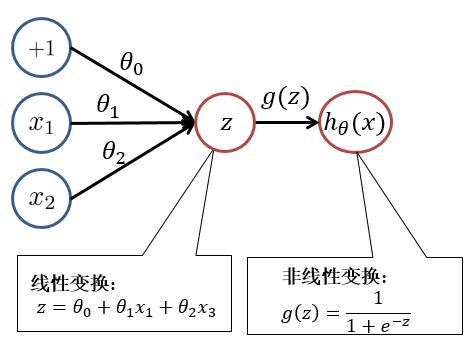
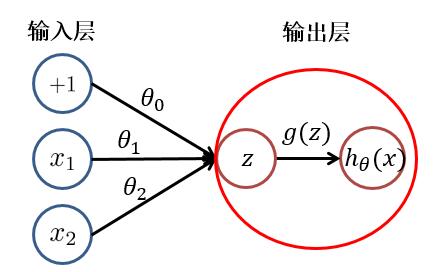
alt text

六、优化器(optimizer)

优化器：会根据损失值，修正神经网路中各层的权重，目标是将损失值减到最小。例如Adam。
对于神经网络的优化算法，主要需要两步：前向传播(Forward Propagation)与反向传播(Back Propagation)
- 前向传播(Forward Propagation)
- 反向传播(Back Propagation)

七、评估指标(metrics)

评估指标：用于评估训练的成效，在训练及评估模型时提供作为参考。例如准确率acc。

八、学习率(Learning rate)

学习率(Learning rate)作为监督学习以及深度学习中重要的超参，其决定着目标函数能否收敛到局部最小值以及何时收敛到最小值。合适的学习率能够使目标函数在合适的时间内收敛到局部最小值。

九、实践中的挑战与解决方案

在神经网络的训练过程中，我们可能会遇到梯度消失和梯度爆炸等问题。梯度消失指的是在反向传播过程中梯度值逐渐减小至零，导致网络无法继续学习；而梯度爆炸则是指梯度值变得过大，导致网络训练不稳定。
为了解决这些问题，我们可以采用一些策略如批量归一化（Batch Normalization）、使用ReLU及其变体作为激活函数、调整学习率等。批量归一化能够保持每层输入的分布稳定，有助于缓解梯度消失和梯度爆炸问题；而ReLU及其变体则因其非线性特性和无梯度限制的特点而备受青睐。