导数、偏导数、方向导数、梯度概念总结

导数从点->坐标轴->特定方向->所有方向的导数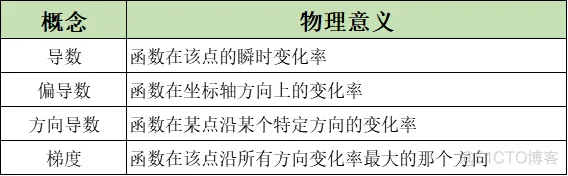
alt text

概念定义

① 导数：
反映的是函数y=f(x)在某一点处沿x轴正方向的变化率。
再强调一遍，是函数f(x)在x轴上某一点处沿着x轴正方向的变化率/变化趋势。
直观地看，也就是在x轴上某一点处，如果f’(x)>0，说明f(x)的函数值在x点沿x轴正方向是趋于增加的；如果f’(x)<0，说明f(x)的函数值在x点沿x轴正方向是趋于减少的。

alt text

② 偏导数：
导数与偏导数本质是一致的，都是当自变量的变化量趋于0时，函数值的变化量与自变量变化量比值的极限。
直观地说，偏导数也就是函数在某一点上沿坐标轴正方向的的变化率。（注意：偏导数的方向不是切线方向，而是沿着自变量坐标轴的方向）

区别在于：
导数，指的是一元函数中，函数y=f(x)在某一点处沿x轴正方向的变化率；
偏导数，指的是多元函数中，函数y=f(x1,x2,…,xn)在某一点处沿某一坐标轴（x1,x2,…,xn）正方向的变化率。
alt text

③ 方向导数：

在前面导数和偏导数的定义中，均是沿坐标轴正方向讨论函数的变化率。
那么当我们讨论函数沿任意方向的变化率时，也就引出了方向导数的定义，即：某一点在某一趋近方向上的导数值。
通俗的解释是：我们不仅要知道函数在坐标轴正方向上的变化率（即偏导数），而且还要设法求得函数在其他特定方向上的变化率，而方向导数就是函数在其他特定方向上的变化率。
alt text

④ 梯度：
梯度的提出只为回答一个问题：函数在变量空间的某一点处，沿着哪一个方向有最大的变化率？
梯度定义如下：函数在某一点的梯度是这样一个向量，它的方向与取得最大方向导数的方向一致，而它的模为方向导数的最大值。
这里注意三点：
　1）梯度是一个向量，即有方向有大小；
　2）梯度的方向是最大方向导数的方向，即函数增长最快的方向；
　3）梯度的值是最大方向导数的值。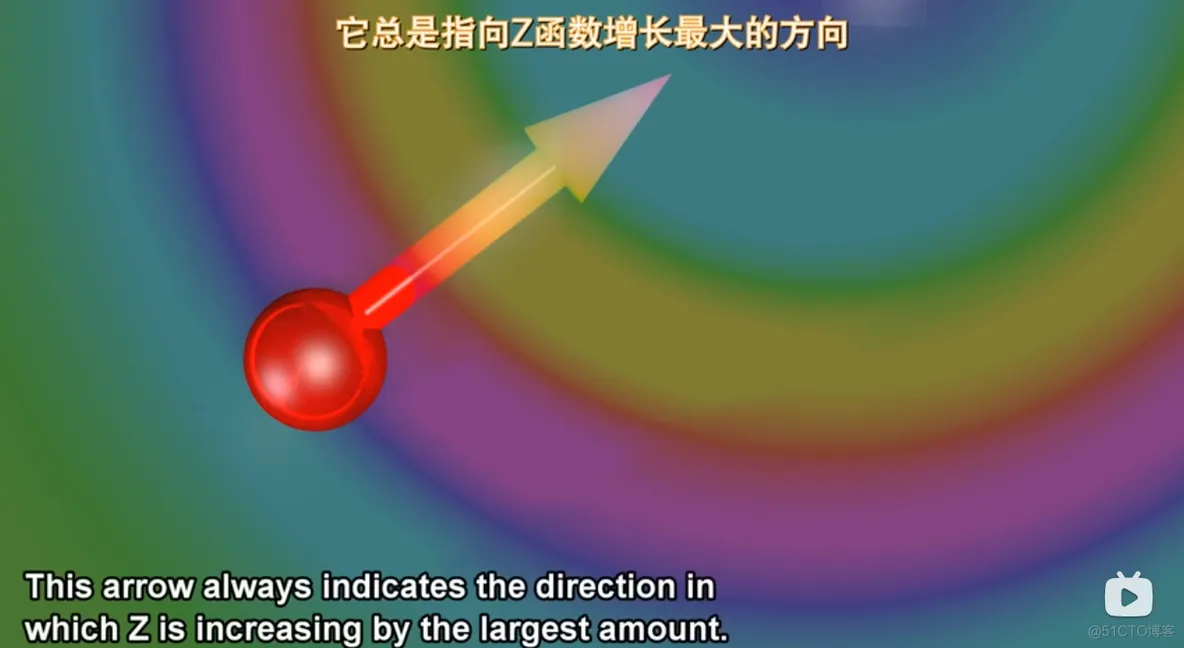
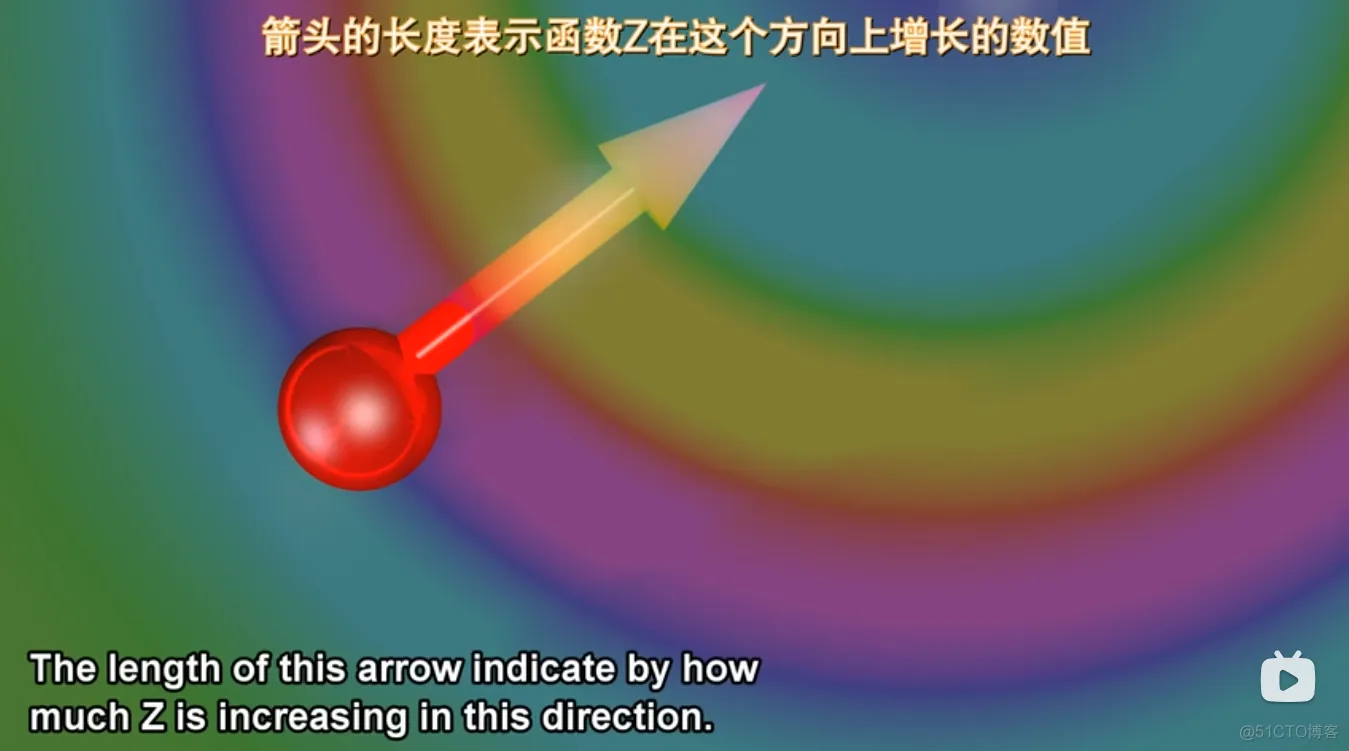
alt text

概念理解

假设一个二元函数z=f(x,y)，可视化后是一个可以呈现在xyz坐标系中的三维图像，求某个方向的偏导数或梯度时，原函数会降一维。
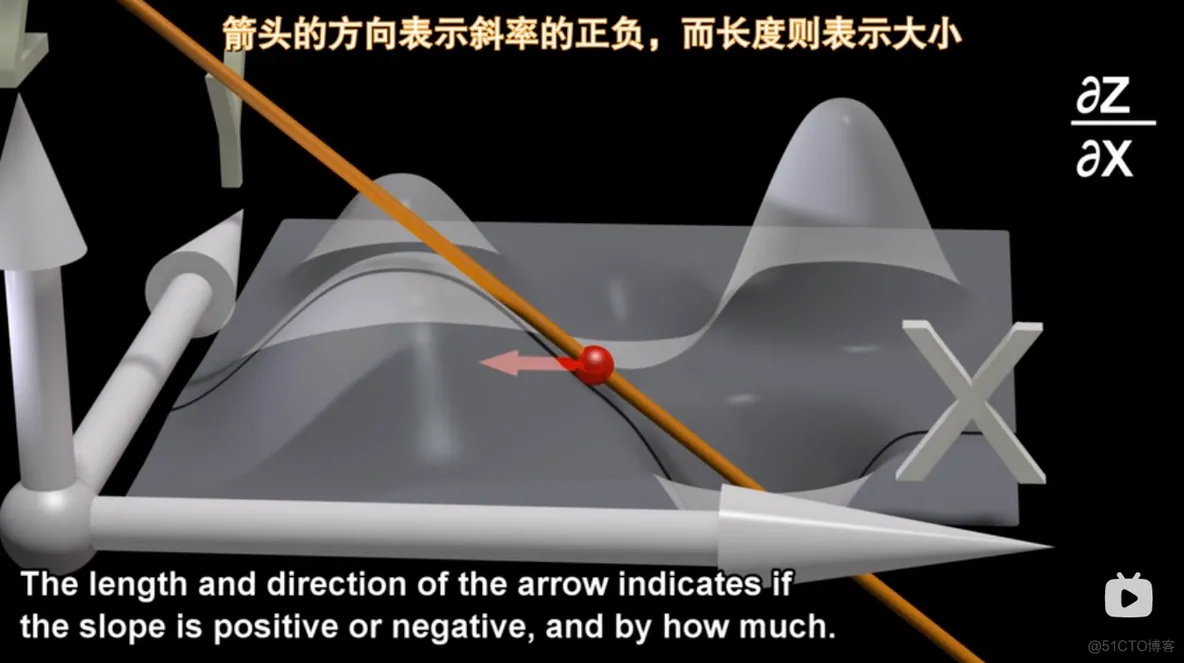
比如，求z对x的偏导数时，y就会为一个固定值，即降低一维，同时偏导数方向是自变量坐标轴方向。
而二元函数z=f(x,y)的梯度方向，是方向导数取最大的方向（函数上升最快的方向），该方向在xy平面内，梯度值的大小为方向导数的最大值。

问：偏导数、方向导数、梯度有何区别？
答：偏导数只能对某一坐标轴方向求导，方向导数可对自变量定义域任意方向求导，而梯度是方向导数值取最大的一个特殊情况。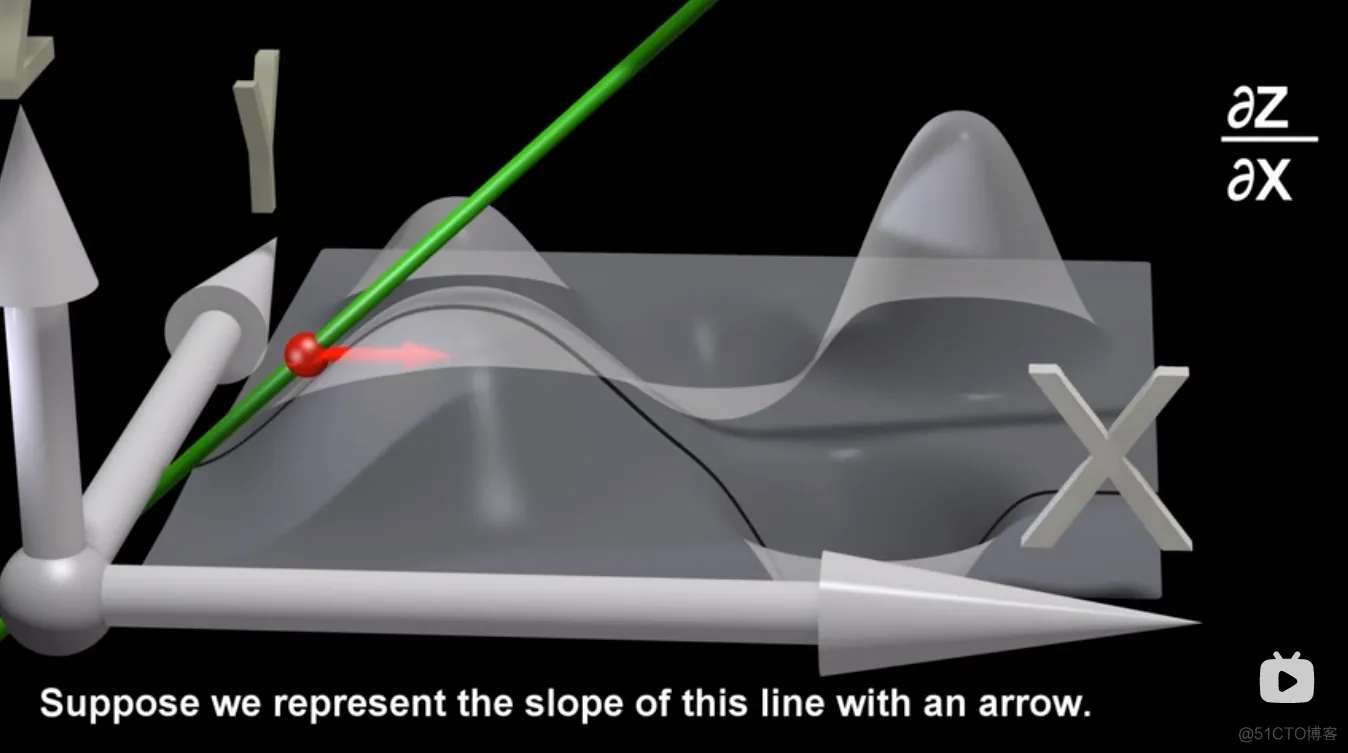
alt text